The Calculated Equation of Motion of a Single Particle in the Electric Fields and Magnetic Fields by Classical Process
Keywords:
Quantum mechanics, Classical action, Path integral, Electric field, Magnetic fieldAbstract
This research aims to present the using of undergraduate math content, solved differential equation problem, to find the equations of motion of a single particle under constant electric fields in the x- and y-axis and uniform magnetic fields in the z-axis by Euler-Lagrange’s equation. We found that the equation of motion corresponds to the matrix method. The relationship between the coefficients in the x-axis and the y-axis is in the form A = -D and B = C. The resulting coefficients are more complex than the assume a variable and matrix methods.
References
Halliday, D. Resnick, R. and Walker, J. (2005), Fundamental of Physics. 7th Edition. John Wiley and Sons, Inc.
วิรุฬห์ สายคณิต. (2552), ทฤษฎีควอนตัม. พิมพ์ครั้งที่ 2. โรงพิมพ์จุฬาลงกรณ์มหาวิทยาลัย. กรุงเทพฯ.
นิคม ชูศิริ. (2541). อินทิกรัลตามเส้นทางของก๊าซอิเล็กตรอนในระบบสองมิติภายใต้อิทธิพลของแรงฮาร์มอนิกส์ สนามไฟฟ้า สนามแม่เหล็ก และศักย์แบบไร้ระเบียบ. มหาวิทยาลัยทักษิณ.
เอกพัน จันผง, อัฏฐชัย ถาวรสุวรรณ, วิทยา ทิพย์อักษร และ นิคม ชูศิริ, (2551), อินทิกรัลตามเส้นทางสำหรับกึ่งฮาร์มอนิกออสซิลเลเตอร. วารสารมหาวิทยาลัยทักษิณ. 11(2), 24-29.
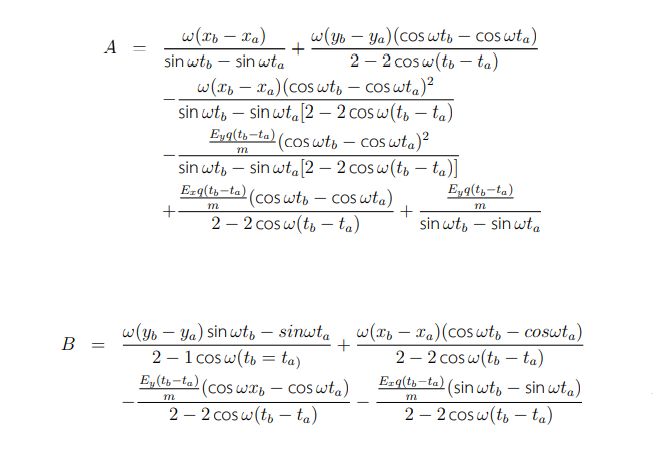
Downloads
Published
Issue
Section
License
Copyright (c) 2022 Journal of KPRU Science Mathematics and Technology

This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
บทความที่ได้รับการตีพิมพ์เป็นลิขสิทธิ์ของวารสาร มรภ.กพ. วิทยาศาสตร์ คณิตศาสตร์ และเทคโนโลยี
ข้อคิดเห็นใดๆ ที่ปรากฎในวารสารเป็นวรรณกรรมของผู้เขียนโดยเฉพาะ ซึ่งมหาวิทยาลัยราชภัฏกำแพงเพชรและบรรณาธิการไม่จำเป็นต้องเห็นด้วย



