การคำนวณหาศักย์ไฟฟ้าภายในตัวนำทรงกลมกลวงรัศมีภายใต้ศักย์ไฟฟ้าบนผิวตัวนำทรงกลมกลวง

อาทิตย์ หู้เต็ม

ผู้แต่ง

อาทิตย์ หู้เต็ม ผู้ประพันธ์บรรณกิจ

คำสำคัญ:

ตัวนำทรงกลมกลวง, ศักย์ไฟฟ้า, ความหนาแน่นประจุไฟฟ้า, สมการลาปลาซ

บทคัดย่อ

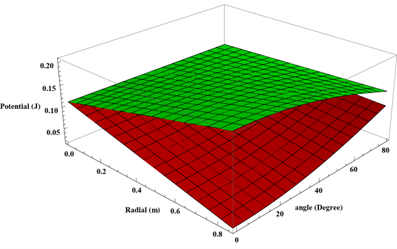
งานวิจัยนี้ต้องการคำนวณหาค่าศักย์ไฟฟ้า $gif.latex?V_{p}(r,\theta&space;)$ และความหนาแน่นประจุไฟฟ้าเหนี่ยวนำ $gif.latex?\sigma_{icl}(\theta&space;)$ ในตัวนำทรงกลมกลวงมีค่ารัศมี $gif.latex?R$ ภายใต้ศักย์ไฟฟ้าบนพื้นผิวตัวนำทรงกลมกลวงทั้ง 2 แบบ คือศักย์ไฟฟ้าแบบโคไซน์ และศักย์ไฟฟ้าแบบไซน์ ซึ่งงานวิจัยนี้ได้ใช้เทคนิคการคำนวณหาศักย์ไฟฟ้าตัวนำทรงกลมกลวงใช้สมการลาปลาซในระบบพิกัดทรงกลมและใช้เทคนิคการอินทิเกรตเพื่อคำนวณหาค่าศักย์ไฟฟ้าของตัวนำทรงกลมกลวง ซึ่งในกรณีที่ 1ศักย์ไฟฟ้าของตัวนำทรงกลมกลวง $gif.latex?V_{p1}{r,\theta}$ จะแปรผันโดยตรงกับค่าพารามิเตอร์สัมประสิทธิ์ค่งคงที่ $gif.latex?\alpha$ และแปรผันโดยตรงกับค่ารัศมี $gif.latex?R$ ในกรณีที่ 2 ศักย์ไฟฟ้าของตัวนำทรงกลมกลวง $gif.latex?V_{p2}(r,\theta)$ จะแปรผันโดยตรงกับค่าพารามิเตอร์สัมประสิทธิ์ค่งคงที่ แต่แปรผกผันกับค่ารัศมี จะแปรผันโดยตรงกับค่าพารามิเตอร์สัมประสิทธิ์ค่าคงที่ $gif.latex?\alpha$ แต่แปรผกผันกับค่ารัศมี $gif.latex?R$ ความหนาแน่นประจุไฟฟ้าเหนี่ยวนำ $gif.latex?\sigma_{ic1}(\theta)$ และ $gif.latex?\sigma_{ic2}(\theta)$ แปรผันโดยตรงกับค่าพารามิเตอร์สัมประสิทธิ์ค่าคงที่ $gif.latex?\alpha$ และมีการสั่นแบบคงที่

References

Lorrain P. and Corson D.R., (1972), Electromagnetic fields and wave (2rd ed.), San Francisco, W.H. Freeman and company, PP.40-61

David J. Griffiths,(1999), Introduction to electrodynamics, (3th ed.). New Jersey, Prentice-Hall International, Inc. pp.58-70

Riley, K.F.,& Hobson, M.P. (2006). Mathematical Methods for Physics and Engineering. (3th ed.). New York: Cambridge University Press.

Generazio E.R., (2017), Electric Potential and Electric Field Imaging, AIP Conference Proceeding 1806, 020025,

Nutnicha Masoongnoen, Piyarat Moonsri, Treenuch Ellis, Sanit Suwanwong and Artit Hutem, (2021), Calculation of Electric Field from Continuous Charge Distribution on Linear Charge Density of Sine Function for Damped