Evaluation of Time-Dependent Displacement of Particle Bound in Anharmonics Oscillator Potential Perturb by Electrostatic External Force via Heisenberg Picture Method
คำสำคัญ:
displacement operator, time-dependent external force, Heisenberg equation of motionบทคัดย่อ
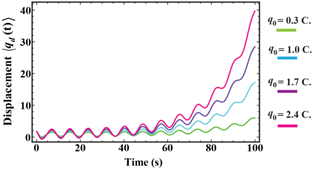
We consider the time-dependent electrostatic force anharmonic oscillator potential in one-dimension. Here, we derive the existing Heisenberg equations of motion from Newton’s second law. We can be used the time-dependent Hamiltonian operator for the time-dependent electrostatic force anharmonic oscillator system. We use the principal of Wronskian method solve for solution of the expectation value of displacement operator for particle bound in anharmonic oscillator potential system. The behavior of the expectation value of displacement operator is wave oscillate depend on the parameter linear frequency, the initial charge, the initial electric, the parameter and .
References
Russell A. (1995). Time-dependent perturbation and exact results for the periodically driven quantum harmonic oscillator, American Journal of Physics, 63, 141-147.
Andrews, M. (2010). Quantum mechanics with uniform forces. American Journal of Physics, 78(12), 1361-1364.
Sang P. K. (2003). Decoherence of quantum damped oscillator, Journal of the Korean Physical Society, 43(4), 452-460
Cordero-Soto, R., Suazo, E., & Suslov, S. K., (2009). Models of damped oscillators in quantum mechanics. Journal of Physical Mathematics, 1, 1-16.
Samuel K. & Peter P. (2013). The velocity operator in quantum mechanics in noncommutative space, Journal of Mathematical Physics, 54, 1021031-10210311
Mark C. P. (2014). Quantum mechanics from Newton’s second law and the canonical commutation relation , European Journal of Physics, 35(045014) pp.1-11
Shigeji F., James M.,& Akira S. (2014). On the Heisenberg and Schrodinger pictures, Journal of Modern Physics, 5, 171-176.
Chew, W. C., Liu, A. Y., Salazar-Lazaro, C. H., & Sha, W. E. I., (2016). Quantum electromagnetics: A new look-part I and part II. IEEE J. Multiscale Multiphys. Comput. Tech, 1, 73-97.
Chew, W. C., Liu, A. Y., Salazar-Lazaro, C. H., & Dong, Y. N., (2019). Hamilton equations, commutator and energy conservation. quantum report, 1, 295-303.
Castanos L.O. & Zuniga-Segundo A. (2019). The forced harmonic oscillator : Coherent states and the RWA, American Journal of Physics, 87, 815-823.
Jussi L. & Jukka L. (2020). The Heisenberg Uncertainty Principle as an endogenous equilibrium property of stochastic optimal control system in quantum mechanics, Symmetry, 12(1533), 1-8.
Moonsri P., Yakaw P. & Hutem A. (2020). CREATION MODEL OF TIME-DEPENDENT LOWERING OPERATOR AND RAISING OPERATOR UNDER TIME-DEPENDENT EXTERNAL DAMPING FORCE SIMPLE HARMONIC OSCILLATOR. PSRU Journal of Science and Technology, 5(3), 52-60.
Nouredine Z. (2001), Quantum Mechanics concepts and applications, NewYork, USA,John Wiley & Sons, 115-125.
Anton Z.C. (2002), Nonrelativistic Quantum Mechanics, Singapore, World Scientific Publishing, 250-255.
Kurt G. & Tung-Mow Y., (2004). Quantum Mechanics : Fundamentals, second edition, NewYork, USA, Springer Publishing, 60-71, 174-1
Downloads
เผยแพร่แล้ว
ฉบับ
บท
License
Copyright (c) 2024 วารสาร มรภ.กพ. วิทยาศาสตร์ คณิตศาสตร์ และเทคโนโลยี
This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
บทความที่ได้รับการตีพิมพ์เป็นลิขสิทธิ์ของวารสาร มรภ.กพ. วิทยาศาสตร์ คณิตศาสตร์ และเทคโนโลยี
ข้อคิดเห็นใดๆ ที่ปรากฎในวารสารเป็นวรรณกรรมของผู้เขียนโดยเฉพาะ ซึ่งมหาวิทยาลัยราชภัฏกำแพงเพชรและบรรณาธิการไม่จำเป็นต้องเห็นด้วย
