Forecasting Engine Oil Change Demand using Holt-Winters for Inventory Planning: A Case Study of a Truck Service Center in Songkhla
Main Article Content
Abstract
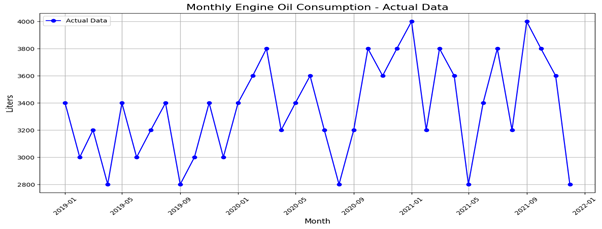
The forecasting demand for oil changes using holt-winters models: a case study of a truck service center in Songkhla province aims to develop a forecasting model for oil change demand for large trucks using Holt-Winters and linear trend models. The study uses monthly data from a truck service center in Songkhla Province from January 2019 to December 2021, comprising 36 months of data. This research compares the performance of several time series forecasting models, including Holt's Linear Trend, Brown's Linear Trend, Damped Linear Trend, Winter's Multiplicative, and Winter's Additive, to determine the most suitable method for future service demand planning. Model performance was evaluated using Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), and Mean Squared Error (MSE). The Winter's Additive model yielded the most accurate forecasts, exhibiting the lowest MAPE of 7.45% (95% Confidence Interval: 5.27 - 9.64) with a p-value of 0.159 between models. This highlights the model's ability to accurately forecast engine oil change demand. The findings are applicable to improving inventory management, resource allocation, service provision, and reducing inventory costs at the Songkhla truck service center.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles published in this journal are copyrighted by the Faculty of Industrial Technology. Nakhon Si Thammarat Rajabhat University
In addition, research results and academic works published in the journal It is the independent opinion of the author. The author is responsible for any legal consequences that may arise from the published article. The editorial team and the journal's production team, we don't always have to agree.
References
Johansen, S. 1992. “Determination of Cointegration Rank in the Presence of a Linear Trend,” Oxford Bulletin of Economics & Statistics. 54(3): pp. 383–397.
Donaldson, W. A. 1977. “Inventory Replenishment Policy for a Linear Trend in Demand—An Analytical Solution,” Journal of the Operational Research Society. 28(3): pp. 663-670; https://doi.org/10.1057/jors.1977.142
Khuanluean, W. and Kanjanasamranwong, P. 2018. “Factors affecting toward Number of Automobile Sales in Thailand,” Journal of Science and Technology, Ubon Ratchathani University. 20(2): pp. 174–184. (in Thai)
Buakla, A., Sangsrichan, C., Mahawan, N., Unnan, C., and Pochan, J. 2022. “A Factor analysis for influencing the development of truck driver skills in the eastern special development zone,” Industrial Technology and Engineering Pibulsongkram Rajabhat University Journal. 15(2): pp. 93–106. (in Thai)
Phuchittrasin, R., Rattanakool, T., Sukkrajang, K., Kaewdee, C., Pansrinual, W., and Sudsomboon, W. 2024. “A Comparison of moving average and simple exponential smoothing methods for predicting engine oil change demand in trucks: A case study in Songkhla province,” Academic Journal of Industrial Technology Innovation. 2(2): pp. 1–12. (in Thai)
Atoyebi, S. B., Olayiwola, M. F., Oladapo, J. O., and Oladapo, D. I. 2023. “Forecasting Currency in Circulation in Nigeria Using Holt-Winters Exponential Smoothing Method,” South Asian Journal of Social Studies and Economics. 20(1): pp. 25-41; https://doi.org/10.9734/sajsse/2023/v20i1689.
Tularam, G. A. and Saeed, T. 2016. “Oil-Price Forecasting Based on Various Univariate Time-Series Models,” American Journal of Operations Research. 6(3): pp. 226-235.
Rodriguez, H., Puig, V., Flores, J. J., and Lopez, R. 2016. “Combined holt-winters and GA trained ANN approach for sensor validation and reconstruction: Application to water demand flowmeters,” in Proceedings of 3rd International Conference on Control and Fault-Tolerant Systems (SysTol), 7-9 September 2016. Barcelona, Spain, pp. 202–207.
Williams, B. M. and Hoel, L. 1999. Modeling and forecasting vehicular traffic flow as a seasonal stochastic time series process. [Online]. Available: https://www.semanticscholar.org/paper/MODELING-AND-FORECASTING-VEHICULAR-TRAFFIC-FLOW-AS-Williams-Hoel/86065d1d235885543cc1973999e6444150c35c7d. Accessed 11 November 2024.
Zhou, W., Tao, H., and Jiang, H. 2022. “Application of a novel optimized fractional grey holt-winters model in energy forecasting,” Sustainability. 14(5): pp. 3118; https://doi.org/10.3390/ su14053118
Rajopadhye, M., Ghalia, M. B., Wang, P. P., Baker, T., and Eister, C. V. 1999. “Forecasting uncertain hotel room demand,” in Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), 2-4 June 1999, San Diego, CA, USA, 3: pp. 1925–1929.
Touama, D. H. Y., 2014. “Application of the statistical analysis for prediction of the Jordanian GDP by using ARIMA time series and holt’s linear trend models for the period (2003-2013),” Mathematical Theory and Modeling. 4(14): pp. 19-27.
Sbrana, G., 2012. “Damped trend exponential smoothing: prediction and control,” Journal of Quantitative Economics. 10 (2): pp. 152–192.
Hansun, S. 2017. “New estimation rules for unknown parameters on holt-winters multiplicative method,” J. Math. Fund. Sci. 49(2): pp. 127.
Starychenko, Y., Skrypnyk, A., Babenko, V., Klymenko, N., and Tuzhyk, K. 2020. “Food security indices in Ukraine: Forecast methods and trends,” Studies of Applied Economics. 38(4): pp. 1–8.
Ahmar, A. S. 2020. “Forecast error calculation with mean squared error (MSE) and mean absolute percentage error (MAPE),” JINAV: Journal of Information and Visualization. 1(2): pp. 94–96.
Robeson, S. M. and Willmott, C. J. 2023. “Decomposition of the mean absolute error (MAE) into systematic and unsystematic components,” PloS one. 18(2): pp. e0279774; https://doi.org/ 10.1371/journal.pone.0279774
Hodson, T. O., Over, T. M., and Foks, S. S. 2021. “Mean Squared Error, Deconstructed,” J Adv Model Earth Syst. 13(12): pp. e2021MS002681; https://doi.org/10.1029/2021MS002681