Robustness of Alternative and Classical Statistics in Two-sample Location Tests for Small Sample Sizes
DOI:
https://doi.org/10.14456/nujst.2023.35Keywords:
two-sample location tests, small sample sizes, bootstrap test, permutation test, parametric test, nonparametric test, robustnessAbstract
When the sample size is small, there is a possibility that the two population groups do not follow assumptions. This includes population distribution and variance. Thus, proper statistical techniques must be selected for generalisation. This article classifies statistical techniques into two types: First, classical statistics consisting of independent t-test, Welch t-test, and exact Wilcoxon-Mann-Whitney test (WMW) and, second, alternative statistics consisting of nonparametric bootstrap t-test (NBTT), nonparametric bootstrap Welch t-test (NBWT), nonparametric bootstrap Welch test based on rank (NBWR), and an exact permutation t-test (PTT). The objective of this study was to propose an alternative statistical method for a small sample size study. The data simulation tested both normal and non-normal distributions including equal and unequal variances. The results revealed that when the populations had normal or non-normal distribution and equal variances, almost all test statistics had robustness at a significance level of 0.05. For a significance level of 0.01, if at least one group had normal distribution, the Welch t-test was the most robust. If there were other distributions, the independent t-test was most robust. For unequal variance, when at least one group had a normal distribution with higher variance than other groups, the Welch t-test could control type I errors in all conditions at significance levels of 0.05 and 0.01. In other cases, it was non-robust. Therefore, if a small sample size is applied, the results must be carefully generalized.
References
Ahad, N. A., Abdullah, S., Lai, C. H., & Ali, N. M. (2000).Relative power performance of t-test and bootstrap procedure for two samples. Pertanika Journal of Science & Technology, 20, 43–52.
Altman, D. G., Gore, S. M., & Gardner, M. J. (1983). Statistical guidelines for contributors to medical journals. British Medical Journal (Clinical Research Ed.), 286, 1489-1493.
Barber, J. A., & Thompson, S. G. (2000). Analysis of cost data in randomized trials: an application of the non-parametric bootstrap. Statistics in Medicine, 19, 3219-3236.
Boos, D. D., & Brownie, C. (1988). Bootstrap p-values for tests of nonparametric hypotheses. Institute of Statistics Mimeo Series No. 1919, North Carolina State University.
Bradley, J. V. (1978). Robustness?. Journal of Mathematical and Statistical Psychology, 31, 321-339.
Bridge, P. D., & Sawilowsky, S. S. (1999). Increasing physicians' awareness of the impact of statistics on research outcomes: comparative power of the t-test and Wilcoxon rank-sum test in small samples applied research. Journal of Clinical Epidemiology, 52, 229-235.
Dwivedi, A. K., Mallawaarachchi, I., & Alvarado, L. A. (2017). Analysis of small sample size studies using nonparametric bootstrap test with pooled resampling method. Statistics in Medicine, 36, 2187-2205.
Efron, B., & Tibshirani, R. J. (1993). An Introduction to the Bootstrap. New York: Chapman & Hall.
Fagerland, M. W., & Sandvik, L. (2009). Performance of five two-sample location tests for skewed distributions with unequal variances. Contemporary Clinical Trials, 30, 490-496.
Haidous, N. H., & Sawilowsky, S. (2013). Robustness and power of the Kornbrot rank difference, signed ranks, and dependent samples t-test. American Journal of Applied Mathematics and Statistics, 1, 99-102.
Hall, P., & Martin, M. (1998). On the bootstrap and two sample problems. Australian Journal of Statistics, 30A, 179-192.
Janusonis, S. (2009). Comparing two small samples with an unstable, treatment-independent baseline. Journal of Neuroscience Methods, 179, 173-178.
Keselman, H. J., Huberty, C. J., Lix, L. M., Olejnik, S., Cribbie, R. A., & Donahue, B. (1998). Statistical practices of educational researchers: An analysis of their ANOVA, MANOVA, and ANCOVA analyses. Review of Educational Research, 68, 350-386.
Mann, H. B., & Whitney, D. R. (1947). On a Test of Whether One of Two Random Variables is Stochastically Larger than the other. Annals of Mathematical Statistics, 18, 50–60
Mundry, R., & Fischer, J. (1998). Use of statistical programs for nonparametric tests of small samples often leads to incorrect P values: examples from Animal Behaviour. Animal Behaviour, 56, 256-259.
Nguyen, D. T., Kim, E. S., Gil, P. R., Kellermann, A., Chen, Y. H., & Kromrey, J. D. (2016). Parametric Tests for Two Population Means under Normal and Non-Normal Distribution. Journal of Modern Applied StatisticalMethods, 15, 141-159.
Posten, H. O. (1982). Two-sample Wilcoxon power over the Pearson system and comparison with t-test. Journal of Statistical Computation and Simulation, 16, 1-18.
Reiczigel, J., Zakarias, I., & Rozsa, L. (2005). A bootstrap test of stochastic equality of two populations. The American Statistician, 59, 1-6.
Ruthsatz, J., & Urbach, J. B. (2012). Child prodigy: A novel cognitive profile places elevated general intelligence, exceptional working memory and attention to detail at the root of prodigiousness. Intelligence, 40, 419-426.
Sawilowsky, S. S., & Hillman, S. B. (1993). Power of the independent samples t-test under a prevalent psychometric measure distribution. Journal of Consulting and Clinical Psychology, 60, 240-243.
Siegel, S. (1956). Nonparametric statistics for the behavioral sciences. New York: McGraw-Hill.
Siegel, S., & Castellan, N. J. (1998). Nonparametric statistics for the behavioral sciences. New York: McGraw-Hill.
Snyder, P. A., & Thompson, B. (1998). Use of tests of statistical significance and other analytic choices in a school psychology journal: Review of practices and suggested alternatives. School Psychology Quarterly, 13, 335-348.
Stonehouse, J. M., & Forrester, G. J. (1998). Robustness of the t and U tests under combined assumption violations. Journal of Applied Statistics, 25, 63-74.
Tanizaki, H. (1994). Power comparison of non-parametric tests: small-sample properties from Monte Carlo experiments. Journal of Applied Statistics, 24, 603-632.
Welch, B. L. (1937). The significance of the difference between two means when the population variances are unequal. Biometrika, 29, 350-362.
Wilcoxon, F. (1945). Individual Comparisons by Ranking Methods. Biometrics, 1, 80-83.
Weber, M., & Sawilowsky, S. (2009). Comparative power of the independent t, permutation t, and Wilcoxon tests. Journal of Modern Applied Statistical Methods, 8, 10-15.
Winter, J. C. F. (2013). Using the Student’s t-test with extremely small sample sizes. Practical Assessment, Research, and Evaluation, 18, 1-12.
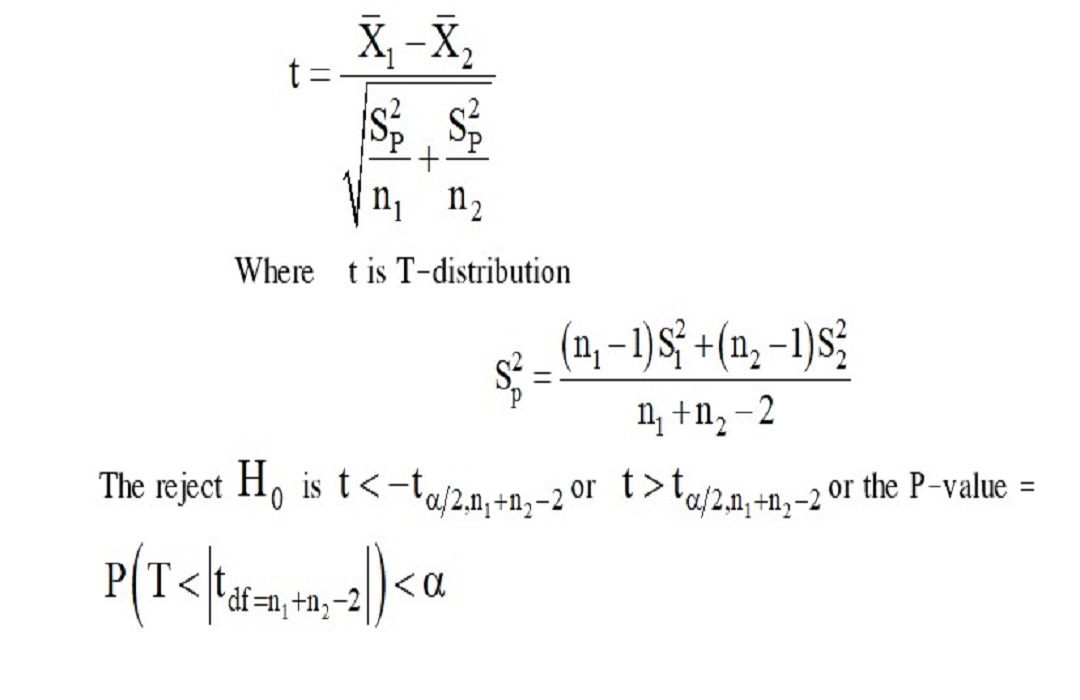
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Naresuan University Journal: Science and Technology (NUJST)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.













