Global Dynamics of Drug Use Model and Its Optimal Control Analysis

Ratchada Viriyapong; Sirapong Nongnamtip

doi:10.14456/nujst.2023.25

Authors

Ratchada Viriyapong Department of Mathematics, Faculty of Science, Naresuan University, Phitsanulok, 65000 Thailand
Sirapong Nongnamtip Department of Mathematics, Faculty of Science, Naresuan University, Phitsanulok, 65000 Thailand

DOI:

https://doi.org/10.14456/nujst.2023.25

Keywords:

drug use, awareness and educational program, family and friends care, basic reproduction number, optimal control

Abstract

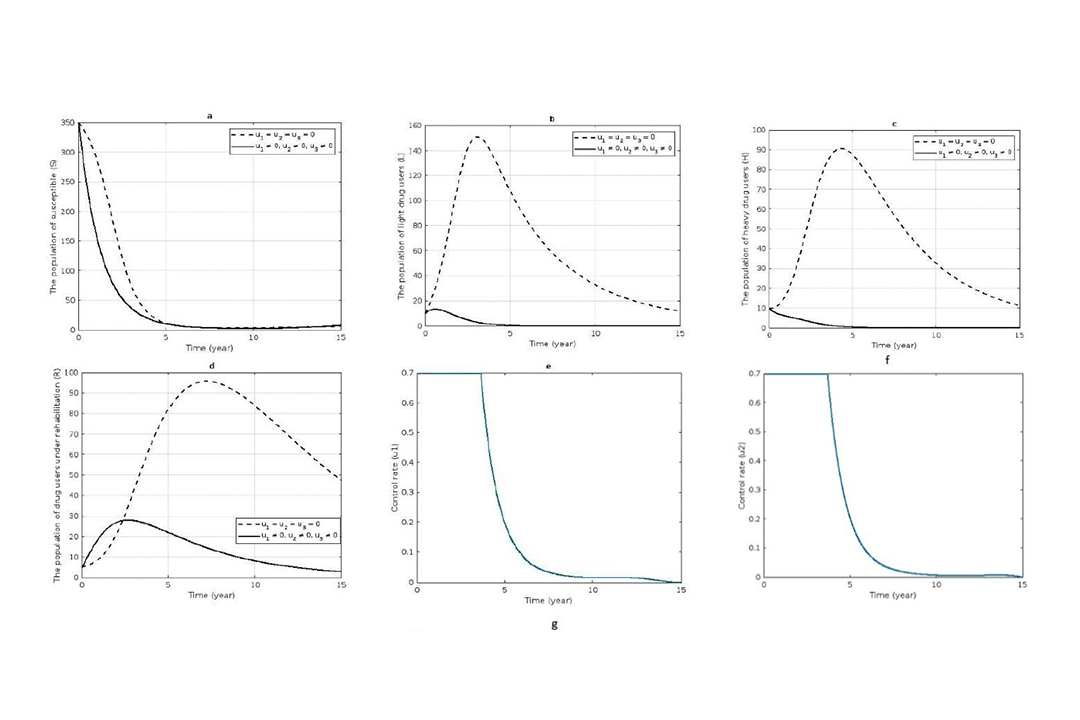
In this paper, we propose and analyze a mathematical model of drug use involving rehabilitation. With our model, we assume that the use of drugs can be initiated by three groups of people; light drug users, heavy drug users and drug users under rehabilitation. In this model, the nonnegativity and boundedness of solutions are verified, and two equilibrium points (drug-free and drug-endemic) are obtained. The basic reproduction number is calculated. We show that each equilibrium point is stable locally and globally under some conditions. Further, an optimal control problem is applied to the model by adding three control variables; awareness and educational program control, family and friends care control, and rehabilitation campaign control. The numerical simulation of this optimal control model is performed, and the results show that each control alone could already reduce the number of drug users for some certain amount, however, a combination of all three controls gives the best result in reducing overall drug use.

References

Binuyo, A. O., & Osuntokun, O. T. (2021). Mathematical modelling of the addiction of drug substance among students in tertiary institutions in Nigeria. Journal of Biomedical Research & Environmental Sciences, 2(9), 851-856.

Butler, G., Freedman, H. I., & Waltman, P. (1986). Uniformly persistent systems. Proceedings of the American Mathematical Society, 96(3), 425-430. https://doi.org/10.2307/2046588

Caulkins, J. P., Gragnani, A., Feichtinger, G., & Trangler, G. (2006). High and low-frequency oscillations in drug epidemics. International Journal of Bifurcation and Chaos, 16(11), 3275-3289. https://doi.org/10.1142/S0218127406016781

Castillo-Chaves, C., Feng, Z., & Huang, W. (2001). On the computation of R0 and its role in global stability. Retrieved from https://ecommons.cornell.edu/bitstream/handle/1813/32146/BU-1553-M.pdf;jsessionid=C2F0E1829E11C268E4B1DB27E666591A?sequence=1

Everingham, S. S., & Rydell, C. P. (1994). Modeling the Demand of Cocaine. Drug Policy Research Centre.

Freedman, H. I., Ruan, S., & Tang, M. (1994). Uniform persistence and flows near a closed positively invariantset. Journal of Dynamics and Differential Equations, 6(4), 583-600. https://doi.org/10.1007/BF02218848

Hafiruddin, M., Fatmawati, F., & Miswanto, M. (2019). Mathematical model analysis of a drug. AIP Conference Proceedings, 2192, 0600101-10. http://dx.doi.org/10.1063/1.5139156

Islam, A. I., & Biswas, H. A. (2020). Optimal control strategy applied to dynamic model of drug abuse incident for reducing its adverse effects. medRxiv. http://dx.doi.org/10.1101/2020.05.02.20088468

Johnston, L. D., O'Malley, P. M., & Bachman, J. G. (1988). Illicit drug use and smoking and drinking by America's high school students and college students and young adults 1975-1987. U.S.: Department of Health and Human Services, Public Health Service.

Kanato, M., & Leyatikul, P. M. P. (2019). Size estimation of substances users population in Thailand 2019. ONCB Journal, 36(2), 37-48. Retrieved from https://nctc.oncb.go.th/download/article/article_20200910112947.pdf

Kanyaa, J. K., Osman, S., & Wainaina, M. (2018). Mathematical modelling of substance abuse by commercial drivers. Global Journal of Pure and Applied Mathematics, 14(9), 1149-1165. Retrieved from http://www.ripublication.com/gjpam.htm

Li, J., & Ma, M. (2018). The analysis of a drug transmission model with family education and public health education. Infectious Disease Modelling, 3(2018), 74-84. https://doi.org/10.1016/j.idm.2018.03.007

Li, M. Y., & Muldowney J. S. (1993). On Bendixson’s criterion. Journal of Differential Equations, 106(1), 27-39. https://doi.org/10.1006/jdeq.1993.1097

Li, M. Y., & Muldowney, J. S. (1996). A geometric approach to global-stablilty problems. SIAM Journal on Mathematical Analysis, 27(4), 1070-1083. https://doi.org/10.1137/S0036141094266449

Mushayabasa, S., & Tapedzesa, G. (2015). Modeling illicit drug use dynamics and its optimal control analysis. Hindawi Corporation Computational and Mathematical Methods in Medicine, 2015, 383154. http://dx.doi.org/10.1155/2015/383154

Njagarah, J. B. H, & Nyabadza, F. (2013). Modelling the role of drug barons on the prevalence of drug epidemics. Mathematical Biosciences and Engineering, 10(3), 843-860. http://dx.doi.org/10.3934/mbe.2013.10.843

Nyabadza, F., & Hove-Musekwa, S. D. (2010). From heroin epidemics to methamphetamine epidemics: Modelling substance abuse in a South African province. Mathematical Biosciences, 225(2010), 132-140. http://dx.doi.org/10.1016/j.mbs.2010.03.002

Olajide, A. J. (2020). Asymptotic stability of illicit drug dynamics with banditry compartment. Applied Mathematics & Information Sciences, 14(5), 791-800. http://dx.doi.org/10.18576/amis/140506

Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V., & Mishchenko, E. F. (1986). In L. S. Pontryagin (Ed), The Mathematical Theory of Optimal Processes. New York: Gordon and BS Publishers.

Rossi, C. (2004). Operational models for epidemics of problematic drug use: The mover-stayer approach to heterogeneity. Socio-Economic Planning Sciences, 38(1), 73-90. https://doi.org/10.1016/S0038-0121(03)00029-6

Samanta, G. P. (2011). Dynamic behaviour for a nonautonomous heroin epidemic model with time delay. Journal of Applied Mathematics and Computing, 35,161–178. https://doi.org/10.1007/s12190-009-0349-z

UNODC. (2021). UNODC World Drug Report 2021: pandemic effects ramp up drug risks, as youth underestimate cannabis dangers. Retrieved from https://www.unodc.org/unodc/en/frontpage/2021/June/unodc-world-drug-report-2021_-pandemic-effects-ramp-up-drug-risks--as-youth-underestimate-cannabis-dangers.html

van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180(1-2), 29-48. https://doi.org/10.1016/S0025-5564(02)00108-6

White, E., & Comiskey, C. (2007). Heroin epidemics, treatment and ODE modelling. Mathematical Biosciences, 208(1), 312-324. https://doi.org/10.1016/j.mbs.2006.10.008

World Drug Report. (2021). United Nations. Retrieved from https://www.unodc.org/unodc/en/data-and-analysis/wdr2021.html